各位老师:
在进入本课程之前,相信你已经完成了课前思考和讨论的问题,因为,我们每一讲都是在思考和讨论的基础上展开。
第一部分 初中课程标准解读
本部分内容包括:等腰三角形、直角三角形和向量
一、等腰三角形
通过观察、实验、操作等活动和对等腰三角形的轴对称性分析,发现和归纳等腰三角形的基本性质,再尝试采用演绎推理方法进行证实;掌握等腰三角形性质的基本运用。
等腰三角形的性质指“等边对等角”、“等角对等边”、“三线合一” 等。可对等腰三角形进行翻转,利用轴对称变换来探索它的性质;在这里,对有关性质的运用限于解释简单的几何问题。
二、直角三角形
▲理解锐角三角比的概念,会求特殊锐角的三角比值。
▲熟悉用计算器求锐角三角比的值。
理解解直角三角形的意义,会用锐角互余、锐角三角比和勾股定理等解直角三角形和解决一些简单的实际问题。
注:锐角三角比只涉及正弦、余弦、正切、余切,注重建立直角三角形的边角关系,对三角比之间的关系不作要求。
三、向量
▲通过实例和位移引入向量的有关概念;掌握向量的要素及向量的表示,理解相等向量、相反向量、平行向量、零向量的意义。
▲通过位移直观认识向量的合成,得出向量加法的三角形法则,归纳加法运算律;再指出向量加法的平行四边形法则和几个向量相加的多边形法则。知道向量加法的交换律与平行四边形的判定和性质定理之间的联系。通过对加法逆运算的讨论引入向量的减法,得出向量减法的三角形法则。会进行向量的加减运算,这里注重于对向量加减运算的直观认识。
第二部分 教学案例剖析
案例一 等腰三角形的教学设计片段

[解答节选]

[分析]
1、 本例将函数与等腰三角形结合起来,培养学生分析问题解决问题的能力。(您可以参考《数学—初高中衔接教材》,第94页)
2、 问题同时提供了数据与图形,学生可以通过对图形的分析简化函数的有关运算,这里体现了数形结合的方法。在解决问题过程中,又对等腰三角形进行了分类,因而渗透了分类讨论思想。
3、 高中数学主要有四种数学思想,即:函数方程思想、等价转化思想、数形结合思想和分类讨论思想。本题三种数学思想得到了体现,因而,为高中数学思想的教学作了很好地铺垫。
[小结]
通过前面案例的剖析,我们已经熟悉了这部分初中知识在高中教学的地位,以及与高中教学要求的落差,如何将这些知识补齐,并加深拓宽,作者也做了精心地练习题的编排。
1.等腰三角形训练题选

[分析]
本练习与例1相呼应,加深学生对几何与函数综合问题的理解。
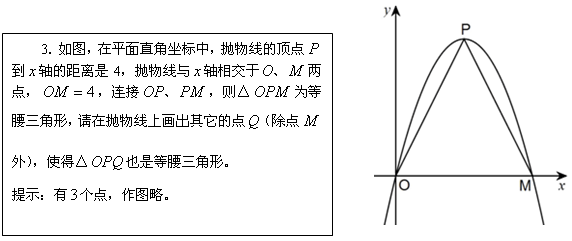
[分析]
作图是高中数学的一项基本技能,高考也经常出现,熟练地作图也反映了学生对知识的深刻理解和具体应用。
案例二 直角三角形的教学设计片段

[分析]
1.例1将三角比的概念置于直角坐标系下,目的是为高中三角比的定义作好准备。(您可以参考《数学—初高中衔接教材》,第97页)
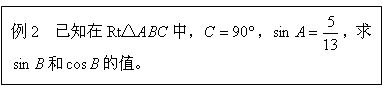
[分析]
2.例2在直角三角形,由已知A的正弦值求其余弦值,是高中诱导分式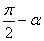 的特例。学员也可设计出用初中的知识方法解决高中问题的其它练习。 的特例。学员也可设计出用初中的知识方法解决高中问题的其它练习。

[分析]
3.例3 是一道实际应用问题,要求学生建立数学模型,进行问题解决。根据实际问题抽象出几何模型,再应用三角知识加以解决,这里体现了数学建模的方法。其实,近几年上海高考多次考查了三角知识的应用题,而本题与2006年上海高考卷第18题类同,这也说明了,有些高考题完全可以应用初中知识加以解决。
[练习选编]
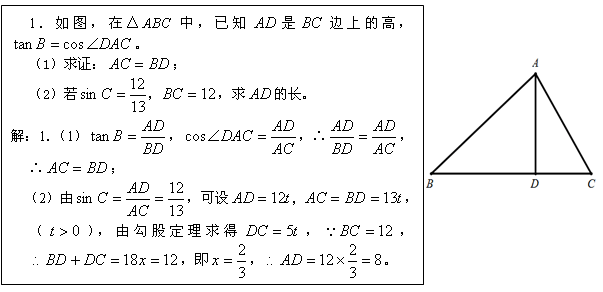
[分析]
应用直角三角形知识解斜三角形,为高中学习解斜三角形提供了一个方法。

[分析]
初中探究型问题是高中研究型问题的基础,这两道练习应用三角知识,探究实际应用问题,既培养了学生的探究意识,也体现了数学教育的目标。
[小结]
直角三角形的教学设计,突出了综合性与前瞻性,以函数、解直角三角形为载体的知识综合运用,培养了学生分析问题解决问题的能力,渗透数学思想;而三角比与直角三角形的结合为高中学习任意角的三角比打下了基础。
案例三 平面向量的教学设计片段
这一单元的教学分为三小节,即:向量、向量的加减法和实数与向量的乘积。
先看向量概念的一道例题
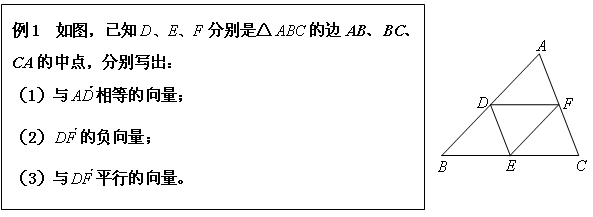
[分析]这是一道对概念的理解辨析题,由于向量有许多概念,通过本例可以检测学生是否理解,并将文字叙述的定义与几何图形相结合,起到了加深对向量概念的理解和辨析。
[教学片段]

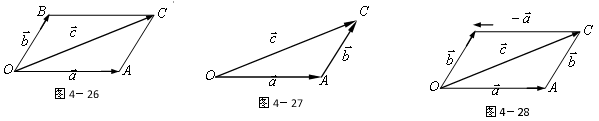
[分析]根据定义,学生只是直观地感受了向量加减法的概念,以及满足的平行四边形、三角形法则,由图像形象地记忆。运算律,也是由实数的运算律迁移而来,学生会想当然地认为这是自然的,教师为了改变这种想当然的思考,对向量的减法由图形作了解释性证明。这为高中学习向量的数量积的运算律、矩阵乘法的运算律作了铺垫。
(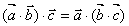 是否成立?并说明理由) 是否成立?并说明理由)

[分析]
1.虽然例3 的证明很简单,但是告诉学生一个结论,即向量的加法运算满足“回路”法则。这种用简单的问题说明重要道理的例题是我们教师需要研究和思考的。
2.例4让学生体会向量问题的证明方法,这也是平面几何“三段论”式证明问题的迁移,例4 看似显然成立,但必须经过严格证明,才能得出结论,这也培养了学生思维的严谨性。
[教案节选]

[分析]
1.通过本例,学生逐步体会到平面几何中的量可以在直角坐标系下表示,而向量具有几何和代数的双重性,虽然初中没有学过向量的坐标表示,但是,教学设计的简单介绍,让学生容易明白向量的坐标表示与几何表示的对应关系,为高中继续学习打下了坚实的基础。
2.向量平行的判定是高中向量教学的一个重点,应用广泛,因而,提前介入,能加深理解。
3.教育部《数学课程标准解读》有这样一段话:“对数学中的重点概念进多次学习,螺旋式上升”,而这一段教学内容的设计,正体现了二期课改的这一理念。(您可以参考《数学—初高中衔接教材》,第101页)
[练习题节选]

[分析]
这两道练习是对重要知识的熟练掌握和加深理解,第3题沟通向量的模与两点间距离的关系。

[分析]
主要训练学生对向量几何运算的理解,为寻找向量代数运算的几何意义作好前期准备。

[分析]
用向量法证明几何题,为学生解决问题提供了又一思路,丰富了解题方法,拓宽了视野,作者这些练习题的编排,为一些初等数学问题解决的多样性提供了更多的选择,也为高中继续学习打下了坚实的基础。
[小结]
1.高中数学引进向量之后,使立体几何的运算更加简便,改变了解析几何的引入体系,因而,向量成为继函数之后,高中数学的另一根主线。所以,扎实的向量基础是学好高中数学的保证。
2.教材备注栏的提示,为学生提供了有效记忆的方法,这也是二期课改新教材的特色之一。(您可以参考《数学—初高中衔接教材》,第103页)
3. 向量的双重性。向量是一个具有几何和代数双重身份的概念,同时向量代数所依附的线性代数是高等数学中一个完整的体系,具有良好的分析方法和完整结构.通过向量的运用对传统问题的分析,可以帮助学生更好地建立代数与几何的联系,也为中学数学向高等数学过渡奠定了一个直观的基础.这方面的案例包括平面几何、立体几何和向量解析几何.
4. “数、量与运算”的扩大。从“数、量和运算”发展的角度理解“向量”,把向量的加法(减法)、数乘以向量看作新的运算,使学生认识到数、量和运算的形式在不断的发展.更为重要的是在教材和教师教学的处理上应该表现出“数、量和运算”的一个发展趋势链,其中数的发展包括正整数(自然数)→零和自然数→正分数(有限小数和无限循环小数)→非负有理数→有理数→无理数(无限不循环小数)→实数→复数,这些“数”所对应的“量”都是一类的,并且至此“运算”的结构没有改变,从整体上看“数”在发展,而“量”及“运算”没有本质的发展.因此向量不是“数”的简单扩大,它所关注的不是“数”的扩大问题,而是“量及运算”的扩大问题.因而在向量的引入时,不宜从代数方程的角度出发,可以从力学的实际背景出发更能体现出“量”的发展.同时还应该强调的是向量代数是以前所有“数的运算”的一个发展,使学生对此问题有一个发展的理解,由此也为今后引入矩阵及其运算做了铺垫. |