例20:用斜二测的作图方法作圆内接正五边形。
[简要步骤]:
(1)作正方形,正方形内接圆以及圆内接正五边形;
(2)作各个顶点的斜二测点(旋转-45°,且缩放1:2);
(3)连结正方形的斜二测点,连结正五边形的斜二测点;
(4)在圆上任取一点,作其斜二测点,选中圆上的点及其斜二测点,作出斜二测点的轨迹,如图6.1。
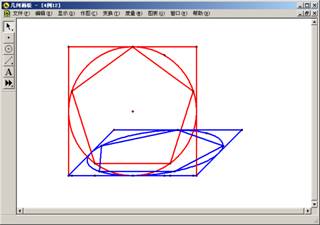
图6.1
例21:如图6.2,求边长为a的正方形中红色区域的面积。
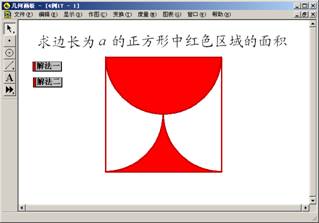
图 6.2
[简要步骤]:
(1)作正方形ABCD及AB、BC、CD、DA的中点E、F、G、H,连结EG、FH得交点I;
(2)以点G为圆心,作半圆DIC,将扇形DIC内部及半圆DIC改为红色;
(3)以点F为圆心,作弧IB,10等分弧IB,得等分点I1、I2、…、I9,依次选中点I1I2 I3I4 I5I6 I7I8I9BEI,作多边形内部,并将此内部及弧IB改为红色,隐藏点I1、I2、…、I9;
(4)以点I为圆心,作弧EF,在弧EF上任取一点J,标记角度EIJ,以点I为旋转中心,将多边形内部及弧IB按标记角度EIJ旋转,得图形①,以EG为对称轴,得与图形①对称的图形②,同时选中图形①和图形②,分别做两个隐藏/显示按钮,并将属性改为总是显示对象、总是隐藏对象,记作显示1、隐藏1;
(5)作点J到F的移动按钮从J→F移动,以及点J到E的移动按钮从J→E移动,隐藏点J和弧EF,并单击隐藏1按钮隐藏图形①和图形②;
(6)以点I为圆心,作弧HE,在弧HE上任取一点K,标记向量EK,将多边形内部及弧IB按标记向量平移,得图形③,以EG为对称轴,得与图形③对称的图形④,同时选中图形③和图形④,分别做两个隐藏/显示按钮,并将属性改为总是显示对象、总是隐藏对象,记作显示2、隐藏2;
(7)作点K到H的移动按钮从K→H移动,以及点K到E的移动按钮从K→E移动,隐藏点K和弧HE;
(8)依次选择显示1、隐藏2、从J→F移动、从J→E移动按钮,作序列按钮,选择依次执行,动作之间暂停1秒;
(9)依次选择显示2、隐藏1、从K→H移动、从K→E移动按钮,作序列按钮,选择依次执行,动作之间暂停1秒;
分别将这2个序列按钮改为解法一、解法二,如图6.3;
(10)隐藏不需要的对象和不需要的按钮。
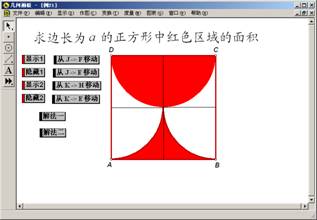
图6.3
例22:在边长为2的正方形四角各剪去边长为x的正方形,然后折成一个容器。求容器容积V与x的函数关系式,并求出容器容积的最大值。
[简要步骤]:
(1)顺次选中原点、单位点,标记为向量;
(2)任取一点C按向量平移,得点C`,再按向量平移,得点C ``,以CC``为一边作正方形,则该正方形的边长为2;
(3)在线段CC `上任取一点F,以CF为小正方形一边,在大正方形的四个角作小正方形,并将剪去四个小正方形后的图形变为红色;
(4)用斜二测方法作折成的容器,如图6.4;
(5)度量点C、F的横坐标xC、xF ,计算xF-xC ,令自变量x=xF-xC ,再计算容积V的值,顺次选中x与V的值,绘制点(x,V);
(6)选中此点与F点,作出此点的轨迹,如图6.4。
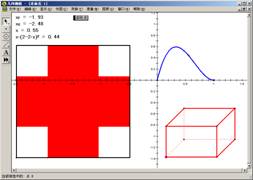 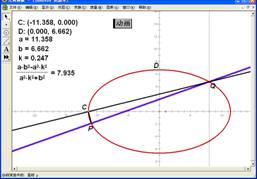
图 6.4 图6.5
例23:已知过椭圆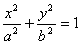 的左顶点(-a,0)的两条相互垂直的弦与椭圆分别相交于点P、Q,则直线PQ具有何特征? 的左顶点(-a,0)的两条相互垂直的弦与椭圆分别相交于点P、Q,则直线PQ具有何特征?
[简要步骤]:
(1)显示坐标轴,在x负半轴、y正半轴上分别取点C、D,分别以原点为圆心,点C、D为圆上的点作大圆和小圆,并由此作出椭圆;
(2)测量点C、D的坐标(-a,0)、(0,b),并算得a、b的值;
(3)在椭圆上任取一点P,作点P的动画按钮;
(4)连结CP,并过点C作CP的垂线l。
由于几何画板无法直接作出直线与轨迹(椭圆)的交点,因此需要间接获得交点。我们可以算出交点的横坐标与纵坐标,于是便可获得交点。本题中,由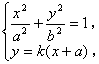 解得 解得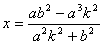 ,其中a、b的值已算得,因此只需再测得垂线l的斜率k,便可算出垂线l与椭圆的交点的横坐标。 ,其中a、b的值已算得,因此只需再测得垂线l的斜率k,便可算出垂线l与椭圆的交点的横坐标。
(5)测量垂线l的斜率,将标签改为k;
(6)计算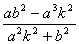 的值,再计算k( 的值,再计算k(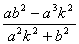 +a)的值,并作出点Q( +a)的值,并作出点Q(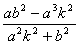 ,k( ,k(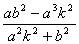 +a)); +a));
(7)作过点P、Q的直线,如图6.5;
(8)单击动画按钮,观察该直线的特征。
可以看到该直线过定点,可以证明该定点为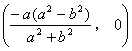 。 。
进一步探索:如果将题目条件改为“已知过椭圆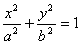 上任意一点的两条相互垂直的弦与椭圆分别相交于点P、Q”,则直线PQ是否还具有同样的特征? 上任意一点的两条相互垂直的弦与椭圆分别相交于点P、Q”,则直线PQ是否还具有同样的特征? |