例17:作摆线。
[简要步骤]:
(1)作线段AB,在线段AB上任取一点C,作线段DE;
(2)以点C为圆心,线段DE为半径作圆,与过点C的线段AB的垂线相交于点F(点F在线段AB的上方),隐藏圆C和垂线;
(3)以点F为圆心,点C为圆上一点作圆;
(4)测量点A、C之间的距离,将标签改为a,测量圆F的半径,将标签改为r;
(5)计算-a/r*1弧度的值,并标记为旋转角度;
(6)以点F为旋转中心,按标记的旋转角旋转点C,得点C`;
(7)同时选中点C和点C`,作轨迹,得摆线,如图5.1。
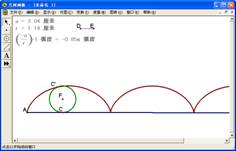
图5.1
例18:作内外摆线(小圆在大圆内)。
[简要步骤]:
(1)以点A为圆心过点B作大圆,并度量大圆A的半径,将度量标签改为R;
(2)在大圆A上任取一点C,连结AC,作弧BC,并度量弧BC的长度,将度量标签改为a。
点C为小圆与大圆的内切点。为了能够改变小圆的大小,且使大圆的半径为小圆半径的整数倍数,故需构造自然数n,不妨设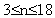 ,再令小圆半径r=R/n即可。 ,再令小圆半径r=R/n即可。
(3)作线段DE,以点D为缩放中心,将点E按1:3缩放,得点E`,再将点E`按1:6缩放,得点E``,隐藏线段DE,连结E`E``,并在线段E`E``上任取一点F;
(4)分别度量D、E和D、F的距离,记为d1和d2,计算round(d1/d2)的值,并将标签改为n,于是可知 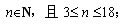
(5)计算半径R/ n的值,得小圆的半径,将标签改为r,将数值r标记为距离;
(6)将点C向右按标记的距离水平平移,得点C`;
(7)以点C为圆心,点C`为圆上的点作圆,交线段AC于点G,隐藏圆C和点C`,再以点G为圆心,点C为圆上的点作圆,得小圆G。
现在只需将弧BC的长度转移到小圆G上。
(8)计算-a/r*1弧度的值,并标记为旋转角度;
(9)以点G为旋转中心,按标记的旋转角旋转点C,得点H;
(10)同时选中点C和点H,作轨迹,将轨迹改成蓝色,得内摆线;
(11)作点H关于线段AC的对称点H`,同时选中点C和点H`,作轨迹,将轨迹改成红色,得外摆线,如图5.2。
改变点F的位置,便可改变n的值,同时也就改变了小圆的大小。
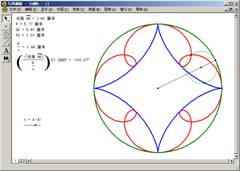 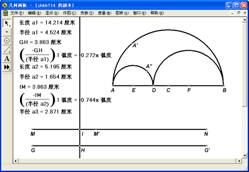
图5.2 图5.3
例19:周长相等。
[简要步骤]:
(1)作线段AB,以线段AB的中点C为圆心作半圆弧AB,在线段AB上取一点D,以线段AD的中点E为圆心作半圆弧AD,以线段DB的中点F为圆心作半圆弧DB;
(2)测量半圆弧AB的长度及半径,并将半圆弧AB的长度标记为距离;
(3)作点G,将点G向右按标记的距离水平平移,得点G`;
(4)连结GG`,在线段GG`上任取一点H;
(5)同例17,将G、H的距离转移到半圆弧AB上,即在半圆弧AB上作出点A`,使弧A`A的长度与G、H的距离相等;
(6)测量半圆弧AD的长度及半径,并将半圆弧AD的长度标记为距离;
(7)将点G和G`向上竖直平移0.5cm,得点M和N,并将点M向右按标记的距离水平平移,得点M`,连结MM`、M`N;
(8)过点H作线段GG`的垂线,交线段MM`于点I,交线段M`N于点J(必要时可移动点H的位置,点I、J不能同时出现,只能出现一个);
(9)同例17,将M、I的距离转移到半圆弧AD上,即在半圆弧AD上作出点A``,使弧A``A的长度与M、I的距离相等,如图5.3;
(10)同例17,将M`、J的距离转移到半圆弧DB上,即在半圆弧DB上作出点D`,使弧D`D的长度与M`、J的距离相等;
(11)选中点H,作动画按钮,隐藏不需要的对象和点的标签。
单击动画按钮,可以看到当点H从点G的位置运动到点G`的位置时,大半圆上的点和小半圆上的点同时从点A的位置运动到点B的位置。由此可知小半圆的周长和等于大半圆的周长。 |