例13:已知两圆内切,求作一圆,使它与大圆内切、与小圆外切,并作出该圆的圆心轨迹。
[简要步骤]:
(1)作射线AM,在射线AM上取一点B,以点A为圆心,点B为圆周上一点作圆AB;
(2)在线段AB上任选一点C,以点C为圆心,点B为圆周上一点作圆CB;
(3)以点B为圆心,点C为圆周上一点作圆与射线AM相交于点D;
(4)以点A为圆心,点D为圆周上一点作圆AD;
(5)在圆AD上任取一点E,连结EA、EC,线段EA与圆AB相交于点F;
(6)作EC的中点G,过点G作线段EC的垂线,交线段EA于点H;
(7)以点H为圆心,点F为圆周上一点作圆HF,选中圆HF,利用显示菜单中的“颜色”选项,将圆HF变为红色,如图4.1。
隐藏不需要的点、线、圆,圆HF就是所求作的圆。
(8)选择点H和点E,利用作图菜单中“轨迹”,得点H的轨迹。
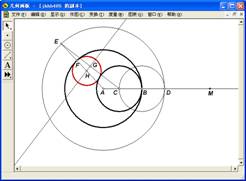
图4.1
选择点E,作动画按钮,跟踪圆HF,你发现了什么?
例14:已知线段MN为定长,且端点M、N分别为x轴、y轴上的自由点。在此基础上作出MN中点的轨迹。
[简要步骤]:
(1)作线段AB,建立坐标系,以原点C为圆心,以线段AB为半径,作圆C;
(2)在圆C上任取一点E,选择点E,作动画按钮;
(3)过点E分别作x轴、y轴的垂线,垂足分别为M、N;
(4)连结MN,如图4.2。
单击动画按钮,可看到点M、N分别在x轴、y轴上运动,且线段MN的长始终不变。
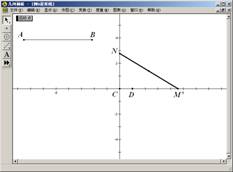 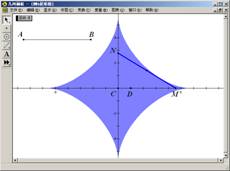
图4.2 图4.3
(5)作线段MN的中点P,选中点P和点E,利用作图菜单中“轨迹”,得点P的轨迹。
(6)选中线段MN,利用显示菜单中的“颜色”选项,将线段MN变为蓝色,选择显示菜单中“追踪线段”选项,单击动画按钮,可看到蓝色的“星型”图形,如图4.3。
例15:作椭圆。过椭圆外一点P作椭圆的切线。
1.利用椭圆的定义作椭圆。
[简要步骤]:
(1)作点A、B,以及线段CD(定长);
(2)以点A为圆心,CD为半径作圆,并在圆A上任意取一点E;
(3)连结AE、BE,并作BE的垂直平分线FG,交BE于点F,交AE于点G;
(4)同时选中点G和点E,作轨迹,如图4.4。
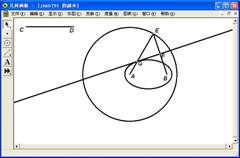 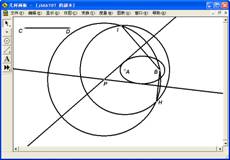
图4.4 图4.5
可以发现直线GF就是椭圆的切线,因此只要直线GF经过点P,也就是要找到圆上一点E的位置即可。
(5)在椭圆外任作一点P;
(6)以点P为圆心,点B为圆上一点作圆,交圆A于点H、I,连结BH、BI;
(7)过点P作BH、BI的垂线,这两条垂线就是过椭圆外一点P所作的椭圆的切线,如图4.5。
2.利用椭圆的参数方程作椭圆。
本例的作图原理就是先计算x = acos t,y = bsin t(-π≤t ≤π),然后根据算得的x、y的值作出点(x,y),最后作出轨迹。
[简要步骤]:
(1)显示坐标轴,在x、y轴上分别取点C、D,测量并计算出点C的横坐标和点D的纵坐标,然后将标签分别改为a和b;
(2)以任意点E为圆心,点F为圆上一点作圆,在圆上任取一点G,测量角FEG的值,并将标签改为t;
(3)将角度设置为弧度制,计算acos t和bsin t的值,并依次选中,画出点H (acost,bsin t);
(4)同时选中点H和点G,作轨迹,如图4.6。
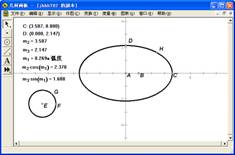 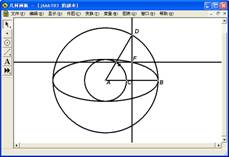
图4.6 图4.7
3.利用椭圆的参数方程的几何意义作椭圆。
[简要步骤]:
(1)作水平线段AB,在线段AB上取一点C,以点A为圆心,分别以点B、C为圆上一点作两个同心圆,在大圆上任取一点D,连结AD,交小圆于点E;
(2)过点D作线段AB的垂线,并过点E作垂线的垂线,两线交于点F;
(3)同时选中点D和点F,作轨迹,如图4.7。
例16:利用“图表”菜单中的“新建参数”、“新建函数”及“绘制新函数”功能,作出函数y=ax2+bx+c的图象。
[简要步骤]:
(1)在绘图窗口中,选择图表菜单中的“定义坐标系”,建立坐标系;
(2)选择图表菜单中的“新建参数”,将名称改为“a”;用同样方法新建参数b和c;
(3)选择图表菜单中的“绘制新函数”,在对话框中输入a*x2+b*x+c(其中输入a、b、c时,只需单击新建的参数a、b、c),然后按确定按钮,得函数f(x)=a*x2+b*x+c的图象;
(4)选中参数a,作动画按钮,将标签改为运动参数a,并将动画范围改为-5到5(如图4.8);用同样的方法作动画按钮“运动参数b”和动画按钮“运动参数c”;
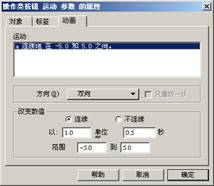 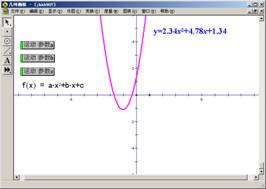
图4.8 图4.9
(5)选择标签/注释工具,作文本“y=”、文本“x2+”和文本“x+”;
(6)顺次选择文本“y=”、参数a、文本“x2+” 参数b、文本“x+”和参数c,选择编辑菜单中的“合并文本”,如图4.9。
单击“运动参数a”动画按钮,或“运动参数b”动画按钮,或“运动参数c”动画按钮,我们可以看到由于参数a,或参数b,或参数c改变而引起的函数图象的改变;也可以依次单击两个动画按钮,或三个动画按钮,看到由于两个或三个参数同时改变而引起的函数图象的改变。 |