怎样使教学更具有时代特征？怎样使教学更适应学生的发展需要？这是我们数学教师面临的重大课题。这就要求我们教师在不断钻研数学知识的同时，还需要学习计算机知识，掌握多媒体数学课件制作的基本方法。对数学教师来说，他们十分容易理解数学软件的各种命令，因此对数学软件也就十分容易上手，而且数学软件本身具有强大的数学功能，能很好地辅助数学教学，帮助学生理解掌握数学概念，促进学生探索研究数学问题。所以，数学教师学习计算机的一些数学软件是很有必要的。
| 环节 |
主题 |
内容概述 |
活动安排 |
| 一 |
基本操作 |
1．当前用于多媒体数学课件制作的计算机数学软件。
2．介绍几何画板工具栏和作图菜单的使用方法，以及作点、线段、射线、直线、圆、弧；过已知点作已知直线的垂线、平行线；作已知角的平分线；度量线段的长度、角的度数、多边形或圆的面积等方法。 |
案例：1．作一条线段的垂直平分线。
2．作一个三角形的内切圆。
3．作相离两圆的内公切线。
4．作一个同已知圆的面积相等的正方形。
讨论： 1.利用作图菜单作图的关键是什么？
2.度量菜单在作图中的作用是什么？
教学材料：工具栏与菜单。 |
| 二 |
动画实现 |
介绍几何画板的动画功能：一个点的动画和多个点在同一对象及不同对象上的动画。介绍几何画板的移动功能。 |
案例：1．利用动画功能，制作一张“光盘”。
2．作地球绕着太阳转，同时月亮绕着地球转的动画。
3．利用变换菜单中“反射”，构造一个万花筒。
4．利用移动按钮实现三类基本的三角形——锐角三角形、直角三角形与钝角三角形之间的相互转变过程的演示。
讨论：1. 如何设置动画按钮？
2. 如何设置点的动画速度？
3．如何设置移动按钮？
4．点的动画与点的移动有何相同点与不同点？
教学材料：几何画板中的辈分。 |
| 三 |
变换迭代 |
介绍几何画板的变换功能：平移、旋转、缩放、反射，以及变换的合成。介绍几何画板的迭代功能。 |
案例： 1．利用“变换”菜单中的“迭代”功能，作出三角形经过“旋转+缩放”变换后的图象。
2．作雪花曲线（Koch曲线）。
3．作Sierpinski三角形。
4．构造勾股树。
讨论：1. 怎样的对象可以进行迭代？
2. 构造勾股树的关键是什么？
教学材料：自定义工具。 |
| 四 |
点的轨迹 |
介绍几何画板的轨迹功能。 |
案例：1．已知两圆内切，求作一圆，使它与大圆内切、与小圆外切，并作出该圆的圆心轨迹。
2．已知线段MN为定长，且端点M、N分别为x轴、y轴上的自由点。在此基础上作出MN中点的轨迹。
3．作椭圆。过椭圆外一点P作椭圆的切线。
4．作函数y=ax2+bx+c的图象。
讨论：1. 如何作出轨迹上的点？
2．点的轨迹与点经过追踪后形成的图案有何区别？
教学材料：利用点的轨迹作极坐标方程的图像。 |
| 五 |
度量转移 |
介绍几何画板的度量转移方法，将直线上的距离转移到圆上，使得线段长度与圆弧长度相等；将圆弧的长度转移到另一个圆上，使得圆弧长度与另一个圆上的圆弧长度相等。 |
案例：1．作摆线。
2．作内外摆线。
3．探索周长是否相等。
讨论：1. 在作摆线时，度量转移需要注意什么？
2. 构思探索周长是否相等课件时应注意什么？
教学材料：龟兔赛跑。 |
| 六 |
应用举例 |
综合利用几何画板的各种功能，制作探索数学问题的课件。 |
案例：1．用斜二测的作图方法作圆内接正五边形。
2．求边长为a的正方形中红色区域的面积。
3．在边长为2的正方形四角各剪去边长为x的正方形，然后折成一个容器。求容器容积V与x的函数关系式，并求出容器容积的最大值。
4．已知过椭圆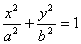 的左顶点（－a，0）的两条相互垂直的弦与椭圆分别相交于点P、Q，探索直线PQ的特征。
讨论：1. 用斜二测方法作图的关键是什么？
2. 制作课件前应注意什么？
教学材料：作具有虚实线的可以旋转长方体。 |
课程简介